LA STORIA DEL CALCOLO DELLE PROPORZIONI
Nicolò Vigna Tavan
Lavoro svolto per il laboratorio di filosofia dei codici logici, con la professoressa Trinchero, presso l’Università di Torino.




RIASSUNTO
La prima applicazione ALGEBRICA di valor medio.
L’origine del calcolo del valor medio proporzionale si fa risalire ai Babilonesi.

HAMMURABI ed i suoi matematici di corte, nel diciassettesimo secolo a.C., elaborarono un sistema di calcolo che si reggeva sul numero 60 come unità fondamentale, utilizzato in ambito topografico, cartografico e di gestione catastale del potere. Essi consideravano, infatti, i numeri 3 e 5 come numeri perfetti ed il numero 60 corrispondeva al risultato del prodotto tra questi due numeri ed il loro valor medio, ovvero il numero 4.
3 : 4 = 4 : 5, 3 x 4 x 5 = 60, il numero-unità di misura fondamentale.
Quella appena descritta fu la prima applicazione ALGEBRICA, nella storia della matematica, relativa al concetto di “valor medio”.
La prima applicazione ARCHITETTONICA di valor medio.
Un secondo sviluppo storico relativo alla teoria delle proporzioni si associa, successivamente, al periodo dell’Antico Egitto.

HEMIUNU, famoso architetto dell’epoca, nella progettazione e nella successiva messa in opera della Piramide di Cheope, realizzò, si narra, con buona approssimazione, il famoso valore della sezione aurea. Il rapporto infatti tra l’altezza delle facciate ed il semilato della base risulta, ancora oggi, di:
186,44/115,183 = 1,619, il numero corrispondente al rapporto aureo.
Questa fu la prima applicazione ARCHITETTONICA, nella storia della matematica, relativo al concetto di “valor medio”.
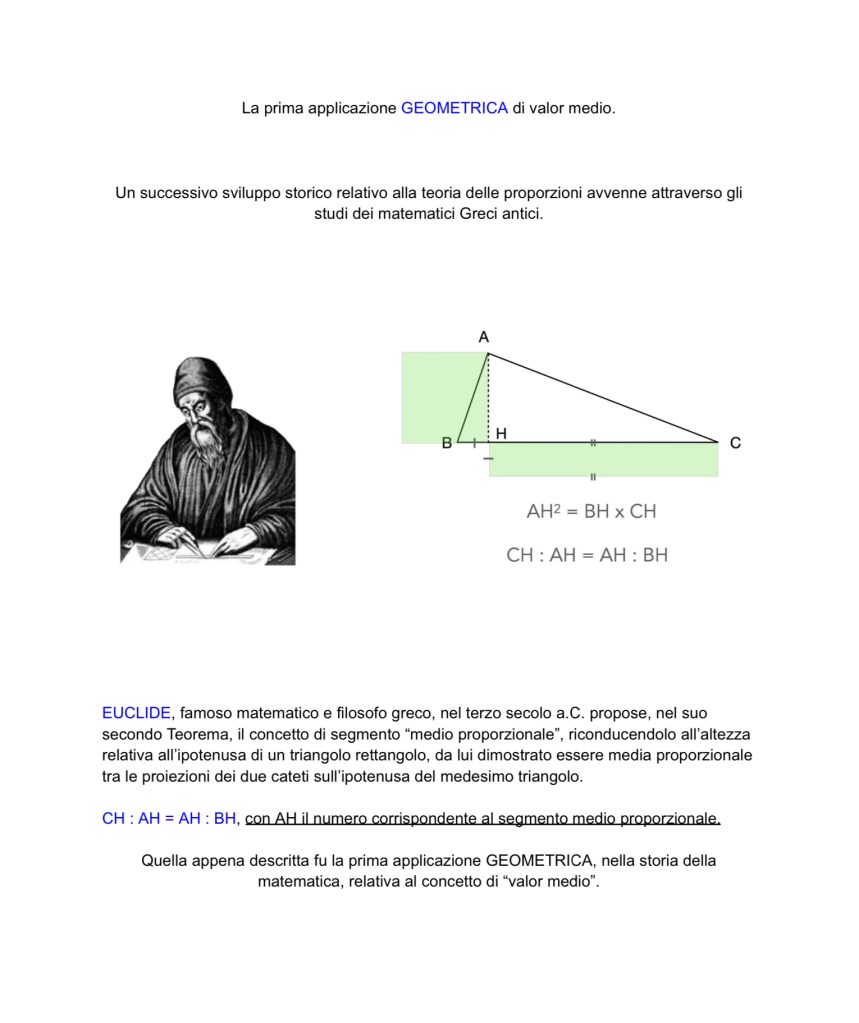
La prima applicazione GEOMETRICA di valor medio.
Un successivo sviluppo storico relativo alla teoria delle proporzioni avvenne attraverso gli studi dei matematici Greci antici.
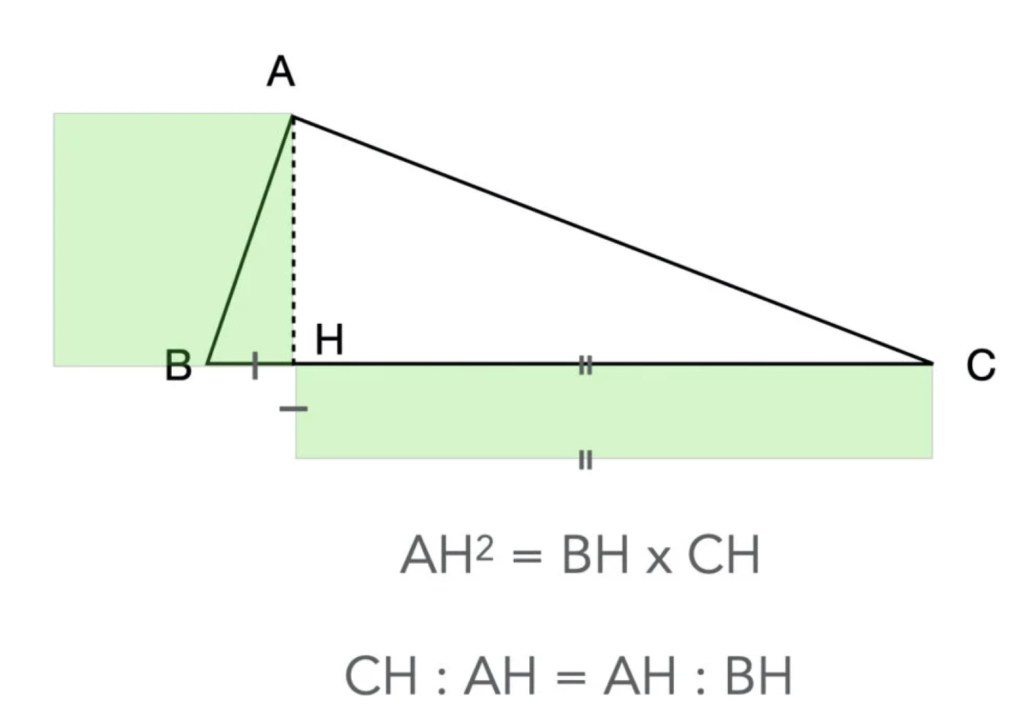
EUCLIDE, famoso matematico e filosofo greco, nel terzo secolo a.C. propose, nel suo secondo Teorema, il concetto di segmento “medio proporzionale”, riconducendolo all’altezza relativa all’ipotenusa di un triangolo rettangolo, da lui dimostrato essere media proporzionale tra le proiezioni dei due cateti sull’ipotenusa del medesimo triangolo.
CH : AH = AH : BH, con AH il numero corrispondente al segmento medio proporzionale.
Quella appena descritta fu la prima applicazione GEOMETRICA, nella storia della matematica, relativa al concetto di “valor medio”.
La prima applicazione ANATOMICA di valor medio.
Un ulteriore sviluppo storico relativo alla teoria delle proporzioni avvenne, altresì, durante il Rinascimento italiano.
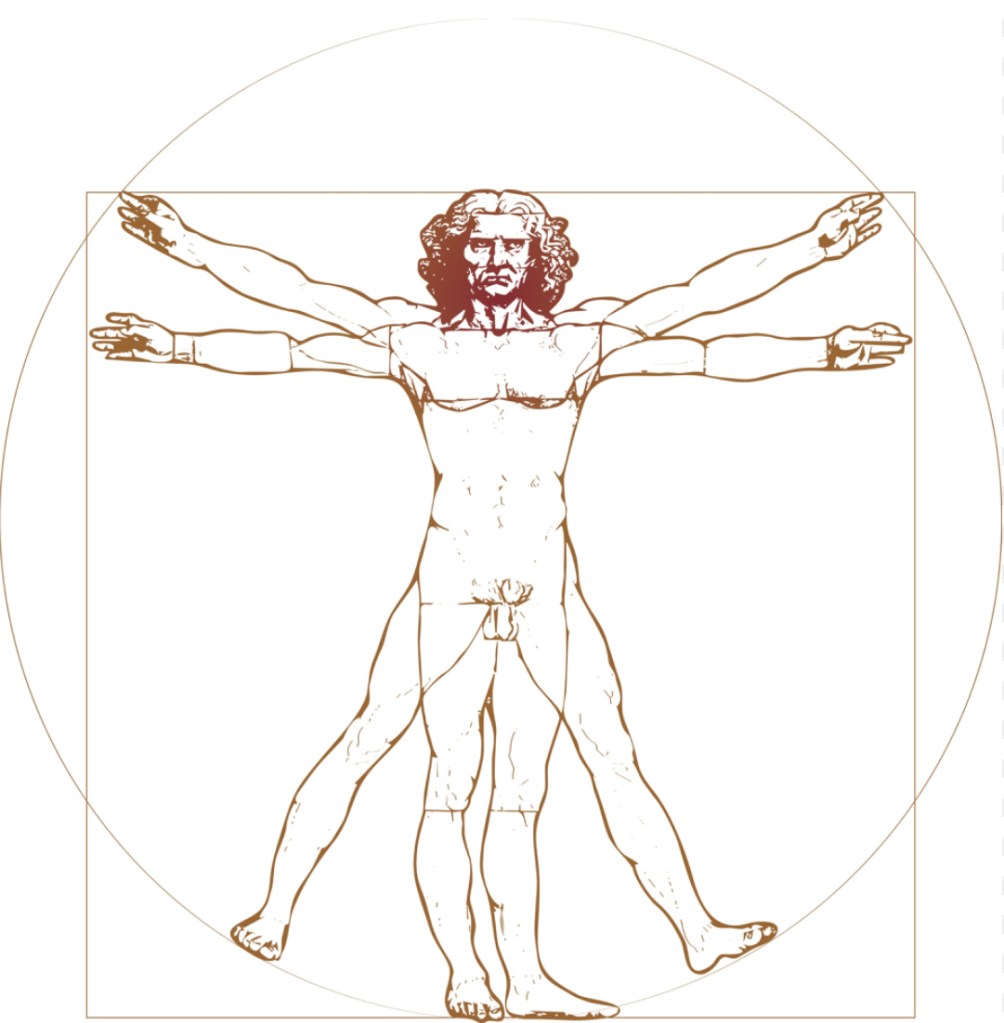
LEONARDO DA VINCI, rifacendosi agli scritti dell’architetto romano Vitruvio, elaborò la teoria dell’uomo come misura di tutte le cose, ed, in particolare, nel suo celebre disegno, con le braccia e le gambe atte a coprire la più ampia area possibile, sottolineò la figura dell’uomo come divisore e come “valor medio” proporzionale tra le figure geometriche del cerchio e del quadrato, ovvero delle due idee grafiche di perfezione rinascimentale.
circonferenza : uomo vitruviano = uomo vitruviano : quadrato, intendendo l’uomo vitruviano come unità di misura medio-proporzionale.
Questa fu la prima applicazione ANATOMICA, nella storia della matematica, relativa al concetto di “valor medio”.
La prima applicazione ASTRONOMICA di valor medio.
Un ultimo sviluppo storico relativo alla teoria delle proporzioni avvenne, nel ‘900, in campo astronomico, in merito alla teoria dei red-shift e dei blue-shift.

EDWIN HUBBLE, astrofisico statunitense, sostenne come, ai margini dell’Universo, se un corpo si muove in avvicinamento rispetto ad un osservatore emette una luce di cromatura blu, viceversa, se un corpo è in allontanamento, emette un colore tendente al rosso. Di conseguenza, se il corpo è fermo, l’osservatore lo vedrà di colore verde, essendo il verde medio proporzionale tra gli altri due colori primari blu e rosso.
rosso : verde = verde : blu, con il color verde inteso come medio proporzionale tra gli altri due colori primari.
Questa fu la prima applicazione ASTRONOMICA, nella storia della matematica, relativa al concetto di “valor medio”.