Lo studio completo di una funzione è uno degli argomenti più importanti del corso di matematica delle scuole superiori ed universitarie ed è alla base di ogni applicazione scientifica, tecnica ed ingegneristica ad ampio spettro.
In questo video-raccolta, andiamo ad analizzare, passo per passo, come si procede per svolgere, nei vari punti, lo studio completo di una funzione generica.
In particolare, ci soffermiamo sullo studio del Numeratore e del Denominatore della Funzione, argomento centrale del nostro esercizio guida.
Il prof. Nicolò Vignatavan, docente di scienze matematiche applicate, illustra, in maniera sintetica, i passaggi chiave dello studio di funzione generico

PUNTI CHIAVE DELLO STUDIO DI FUNZIONE:
CONDIZIONI di ESISTENZA E
Il primo punto che dobbiamo andare ad affrontare è, necessariamente, lo studio delle CONDIZIONI DI ESISTENZA o CAMPO DI ESISTENZA “E” della funzione. Riassumendo, in questo primo punto si tratta di andare a verificare per quali valori di x la nostra funzione esiste, sia a livello algebrico che a livello grafico, e per quali altri invece essa non esiste.

[Al minuto 00.34 del video]
STUDIO del NUMERATORE N e del DENOMINATORE D
Il passaggio successivo che dobbiamo affrontare è lo STUDIO DEL NUMERATORE e DEL DENOMINATORE della nostra funzione. Occorre porre il Numeratore N>=0 ed il Denominatore D>0. In questo modo otteniamo i risultati che ci permettono di compilare la nostra tabella della soluzioni (dei segni).

[Al minuto 01.25 del video]
COMPILAZIONE della TABELLA dei SEGNI
Questo passaggio consiste nella stesura e nella compilazione della così chiamata TABELLA DEI SEGNI: al suo interno occorre immettere le soluzioni ricavate dallo studio delle Condizioni di esistenza, del Numeratore e del Denominatore della nostra funzione.

[Al minuto 03.50 del video]
RAPPRESENTAZIONE delle AREE di INFLUENZA del GRAFICO sul PIANO CARTESIANO
Questo passaggio consiste nella rappresentazione delle AREE DI INFLUENZA della funzione sul piano cartesiano. Disegnato il piano di asse verticale y ed orizzontale x, occorre, considerando i tratti di positività e negatività riconosciuti nelle soluzioni della tabella dei segni, andare ad evidenziare le aree di piano positive e negative rispetto agli assi nelle quali il grafico esisterà e quelle in cui esso non esisterà.

[Al minuto 08.43 del video]
STUDIO delle INTERSEZIONI con gli ASSI CARTESIANI della FUNZIONE
Questo punto consiste nell’andare ad individuare i punti di intersezione del grafico della funzione con gli assi cartesiani. Per ottenere questo risultato occorre porre a sistema la funzione rispettivamente con l’asse x ed in seguito con l’asse y.
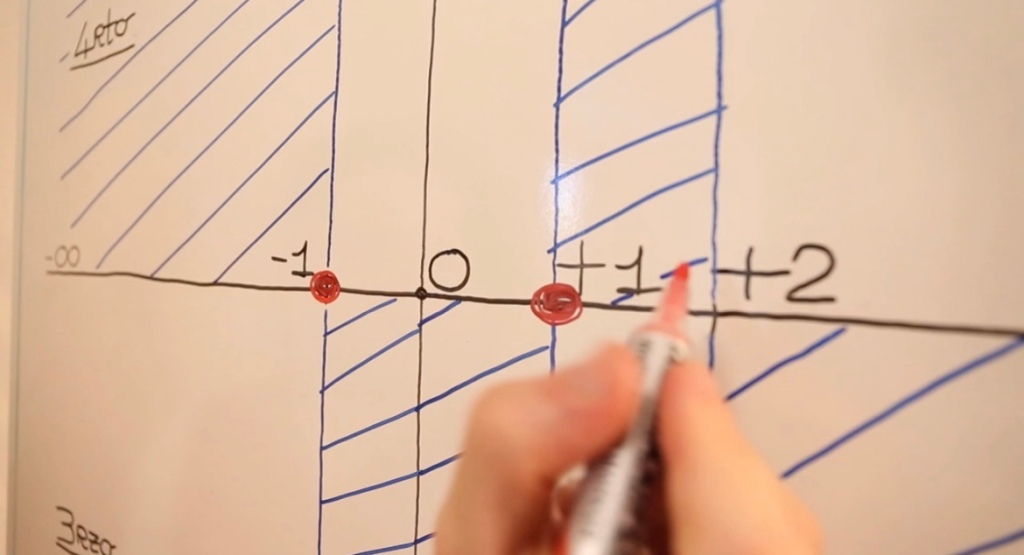
[Al minuto 11.51 del video]
CALCOLO dei LIMITI al FINITO della nostra funzione
Questa è una tappa fondamentale all’interno del nostro percorso di sviluppo dello studio di funzione. Si tratta di andare a calcolare i limiti al finito, ovvero quelli nell’intorno dei punti esclusi dalle condizioni di esistenza, dove il nostro grafico non potrà passare e non esisterà.

[Al minuto 15.18 del video]
CALCOLO dei LIMITI all’INFINITO della nostra funzione
Dopo aver calcolato i limiti al finito, occorre calcolare quelli all’infinito, per studiare l’andamento del grafico della nostra funzione nelle aree di estremità del piano cartesiano rispetto all’asse x.

[Al minuto 20.18 del video]
STUDIO degli ASINTOTI della FUNZIONE
Questo punto riguarda il riconoscimento degli eventuali asintoti presenti lungo il grafico della nostra funzione. Gli asintoti possono essere di tipologia orizzontale, verticale o obliqua ed è fondamentale tracciarli per poter disegnare in maniera precisa il grafico della nostra funzione.

[Al minuto 24.15 del video]
DISEGNO COMPLETO del GRAFICO della nostra funzione
Siamo arrivati alla fine del nostro esercizio: ecco l’ultimo punto, l’atto conclusivo del nostro lavoro, ovvero il disegno del grafico della funzione sul piano cartesiano. Avendo ora tutte le informazioni e le coordinate utili, nel dettaglio, possiamo finalmente completare l’opera e redigere il grafico il maniera completa.
